I want to share some neat intuition that I came across in David Mackay’s text book about Jensen’s inequality. Jensen’s inequality is a simple enough inequality that crops up frequently in machine learning, especially in variational methods, when one wants to bound an expectation.

Jensen states that:

for any convex function f.

Writing this out more verbosely it states (for discrete distributions):

Where $p_i = P(X = x_i)$.

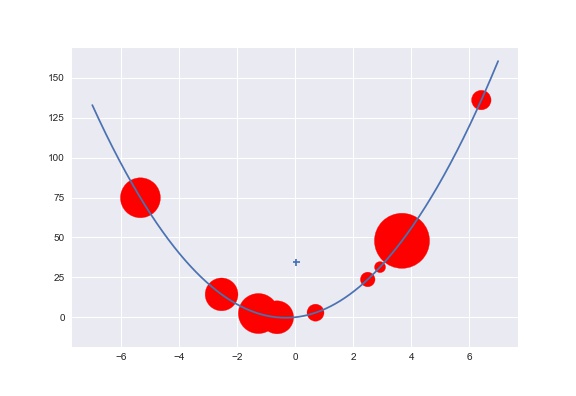
Now if we imagine that we place a mass of size $p_i$ along the curve $f$ at each of the coordinates $(x_i, f(x_i))$ then $\sum f(x_i) p_i$ is simply the y-coordinate of the centre of mass (remember $\sum p_i = 1$). The $\sum x_i p_i$ is the x-coordinate.

Viewed this way, all that Jensen’s inequality says is that for any convex curve, the centre of mass of masses placed on the curve, must lie above the curve. That seems intuitively obvious to me in a way that isn’t at first clear from staring at the inequality.

The picture below shows some masses placed on a convex curve along with their centre of mass in 2-d. It’s hopefully pretty obvious that the centre of mass of these masses has to lie above the curve (and its shown with a cross).